728x90
반응형
Step, Sigmoid, Tanh, ReLU, Leaky ReLU, PReLU, ELU, Maxout, Softmax Function
Github Link 🔽 자세한 코드
gggggeun/study
Contribute to gggggeun/study development by creating an account on GitHub.
github.com
1. 계단함수 Step function
import numpy as np
import matplotlib.pyplot as plt
import math
# 샘플데이터
x = np.array([-1, 1, 2])
# 0 보다 클 경우 1
y = x>0
y = y.astype(np.int)
def step_function(x) :
return np.array(x>0, dtype=np.int)
# 그래프 그리기
x = np.linspace(-1, 1, 100)
plt.step(x, step_function(x))
plt.grid(which='major')
plt.show()
- 0보다 큰 경우 1 출력, 0보다 작은 경우 0 출력 (Binary)
- 직관적이다.
- 모델 Optimization 과정에서 미분을 해야하는데 계단함수는 미분이 되지 않아 딥러닝 모델에는 사용할 수 없음.
2. 시그모이드 함수 Sigmoid Function
* 미분 수학적 풀이 https://towardsdatascience.com/derivative-of-the-sigmoid-function-536880cf918e
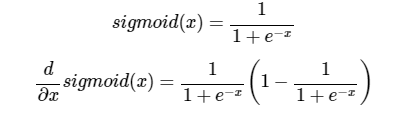
# 시그모이드 함수
def sigmoid(x) :
return 1/(1+np.exp(-x))
# 시그모이드 함수의 도함수 유도
def sigmoid_prime(x):
sig = sigmoid(x)
return sig * (1 - sig)
# 시그모이드 함수, 도함수 그래프 생성
x_range = np.arange(-10, 10, 0.2)
y_range = np.array([sigmoid(x) for x in x_range])
y_prime = np.array([sigmoid_prime(x) for x in x_range])
plt.plot(x_range, y_range, label='sigmoid')
plt.plot(x_range, y_prime, label='sigmoid_prime')
plt.grid(which='major')
plt.legend()
plt.show()
- 눕힌 s자 모양. (A′=A(1−A)) 로 미분이 간결하게 되어 코드로 구현하기 쉽고 입문 단계에서 꼭 다루는 함수이다.
- 시그모이드 함수를 미분하면 최대치가 0.25 -> 1보다 작아 계속 곱하면 0에 가까워짐
- x가 0일때 기울기가 최대가 된다. 그 미분값은 1/4이다.(최대치)
- 모든 실수 값을 0보다 크고 1보다 작은 미분 가능한 수로 변환하는 특징을 갖기 때문에, Logistic Classification과 같은 분류 문제에 많이 사용됨.
- 역전파 알고리즘에서 여러 층을 거칠수록 기울기가 작아져 처음 층까지 전달되지 않는 기울기 소실(vanishing gradient) 문제가 발생해 가중치를 수정하기 어려워짐.
- 1~2개 Layer에서는 사용할 수 있겠지만 Deep한 학습법에서는 비추.
3. 하이퍼블릭 탄젠트 함수 Tanh Function

#탄젠트 함수
def tanh(x) :
return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
# 탄젠트 도함수
def tanh_prime(x):
tan = tanh(x)
return 1-tan**2
# 하이퍼블릭 탄젠트 함수, 도함수 그래프 생성
x_range = np.arange(-10, 10, 0.2)
y_range = np.array([tanh(x) for x in x_range])
y_prime = np.array([tanh_prime(x) for x in x_range])
plt.plot(x_range, y_range, label='tanh')
plt.plot(x_range, y_prime, label='tanh_prime')
plt.grid(which='major')
plt.legend()
plt.show()
- sigmoid와 모양이 비슷하지만 그래프 위치와 기울기가 다름.
- sigmoid fuction을 보완하고자 나온 함수.
- 입력신호를 -1과 1 사이 값으로 normalization해준다.
- 거의 모든 방면에서 sigmoid보다 성능이 좋다.
- 기울기 최대인 x가 0인 지점의 미분값은 1이된다. 이것도 Gradient Vanishing 문제가 발생한다.(하지만 sigmoid 함수보다는 덜하다.)
4. 렐루 함수 ReLu (Rectified Linear Unit)
* 관련 문서 : https://towardsdatascience.com/neural-networks-an-alternative-to-relu-2e75ddaef95c

# 렐루 함수
def rectified(x):
return max(0.0, x)
# ReLU 도함수
def rectified_prime(x):
if x>0:
return 1
else:
return 0
# 그래프
x_range = np.arange(-10, 11)
y_range = np.array([rectified(x) for x in x_range])
y_prime = np.array([rectified_prime(x) for x in x_range])
plt.plot(x_range, y_range, label='relu')
plt.plot(x_range, y_prime, label='relu_prime')
plt.grid(which='major')
plt.legend()
plt.show()
- 토론토 제프리 힌튼 교수
- 시그모이드 함수의 대안으로 떠오르며 현재 가장 인기있는 활성화 함수
- x가 0보다 작을 때는 모든 값을 0으로 처리, 0보다 큰 값은 x 그대로 사용.
- 단순해보이지만 x가 0보다 크기만 하면 미분값이 1이 된다.
- 따라서 여러 은닉층을 거치며 곱해지더라도 맨 처음 층까지 사라지지 않고 남아있을 수 있다.
- 하지만 마지막의 결과 값을 출력하는 Output layer에서는 sigmoid 함수를 사용하게 된다. 0과 1 사이로 나와야 하기 때문에.
- exp() 함수를 사용하지 않아 sigmoid나 tanh보다 1.5배, 2배 빠르게 학습이 된다고 한다.
- Output으로 0이 많아 계산하는 시간과 메모리가 적은 장점이 있다. 또한 잠재적으로 overfitting을 막아준다고 한다. 같은 이유의 단점으로는 몇몇 가중치는 절대 업데이트 되지 않아 뉴런이 죽는 현상(Dying ReLU)이 발생한다.
- 경계가 없기에 가중치가 제대로 초기화되지 않은 경우 Gradient Exploding 문제가 생길 수 있음.
- 이후 ReLU의 0이 되는 순간을 완화한 softplus 함수 등 렐루를 변형한 함수도 개발됨
5. 리키 렐루 Leaky ReLU (+PReLU)


# Leaky ReLU 함수 & 도함수
a=0.2 # parameter 조정가능(=PReLu)
def leaky_relu(x):
if x>0:
return x
else:
return a*x
def leaky_relu_prime(x):
if x>0:
return 1
else:
return a
# 하이퍼블릭 탄젠트 함수, 도함수 그래프 생성
x_range = np.arange(-3., 3., 0.1)
y_range = np.array([leaky_relu(x) for x in x_range])
y_prime = np.array([leaky_relu_prime(x) for x in x_range])
plt.plot(x_range, y_range, label='Leaky ReLU')
plt.plot(x_range, y_prime, label='Leaky ReLU (Derivative)')
plt.ylim([-1.0, 3.0])
plt.xlim([-3.0, 3.0])
plt.grid(which='major')
plt.legend()
plt.show()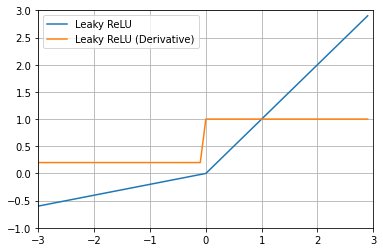
- x가 음수인 경우 미분값이 0이 되지 않는다.
- ReLU의 Dying ReLU(뉴런이 죽는 현상)문제를 해결하기 위해 나온 함수.
- Gradient exploding 문제를 방지하진 않는다.
- ELU보다 계산이 더 효율적이다.
- PReLU(Parametric ReLU)는 음수에 대한 gradient를 변수(a)로 두고 학습을 통하여 업데이트 시키자는 컨셉.
6. ELU (Exponential Linear Unit)

# Leaky ReLU 함수 & 도함수
a=1 # parameter 조정가능
def elu(x):
if x>0:
return x
else:
return a*(np.exp(x)-1)
def elu_prime(x):
if x>0:
return 1
else:
return a*np.exp(x)
# 하이퍼블릭 탄젠트 함수, 도함수 그래프 생성
x_range = np.arange(-3., 3., 0.1)
y_range = np.array([elu(x) for x in x_range])
y_prime = np.array([elu_prime(x) for x in x_range])
plt.plot(x_range, y_range, label='ELU')
plt.plot(x_range, y_prime, label='ELU (Derivative)')
plt.ylim([-1.0, 3.0])
plt.xlim([-3.0, 3.0])
plt.grid(which='major')
plt.legend()
- ReLU의 모든 장점을 포함하며 Dying ReLU 문제를 해결함.
- Gradient exploding 문제를 방지하진 않는다.
- 출력 값이 거의 ZERO-CENTERED에 가까우며, 일반적으로 ReLU와 다르게 지수 함수를 계산하는 비용이 발생한다. (Zero-centered란 그래프의 중심 0인 형태로 함숫값이 양수 혹은 음수에만 치우치지 않고 실수 전체에서 나타나는 형태를 의미)
- Leaky ReLU보다 수렴이 빠르다.
7. Maxout

- ReLU의 장점을 모두 가지며, ReLU의 단점인 Dying ReLU 문제 또한 해결한다.
- 하지만 계산해야 하는 양이 많고 복잡하다는 단점이 있다.
8. 소프트맥스 함수 Softmax Function



- 다범주 분류기. 일반적으로 출력노드의 활성함수로 소프트맥스 함수를 사용함.
- 범주 수만큼의 차원을 갖는 입력벡터를 받아 확률로 변환해줌.(합이 1)
- 가장 큰 출력 값의 클래스가 확률이 가장 높은 것으로 이용됨.
- 벡터의 각 원소를 정규화하기 위해 입력 값을 모두 지수값으로 바꿈.(지수함수를 사용하면 가중치를 더 커지게 하는 효과가 있음.)
- 한 클래스의 근거(evidence)가 작을 때 그 클래스의 확률도 더 낮아짐.
- 자신의 가중합 뿐 아니라 다른 출력 노드들의 가중 합도 고려.
- 예측이 잘 이루어지지 않으면 여러 레이블이 비슷한 확률을 가지게 될 수도 있음.
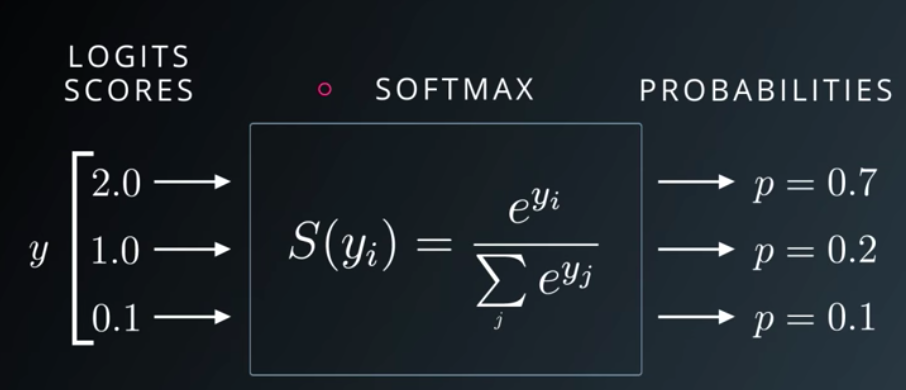
* ReLU, LReLU, ELU 그래프 비교

* 활성함수 그래프 비교

728x90
반응형
'딥러닝 (Deep Learning) > 딥러닝 기초' 카테고리의 다른 글
| 딥러닝의 개념과 동작 원리 (0) | 2021.04.22 |
|---|---|
| '표현(representation)을 학습하다' 의미 (0) | 2021.04.21 |
| 신경망의 구성, 구조 with python (0) | 2021.04.11 |
| 퍼셉트론의 한계, XOR (0) | 2021.04.08 |
| 신경망 관련 개념 정리 (0) | 2021.04.08 |