퍼셉트론은 Frank Rosenblatt이 1957년 고안한 알고리즘입니다. 그러나 인공지능 선구자 Marvin Minsky 교수가 퍼셉트론의 한계에 대해 1969년 논문으로 발표했습니다.
퍼셉트론의 한계에 대해서는 XOR(exclusive OR)문제로 풀어볼 수 있습니다.
XOR 문제는 디지털 논리회로에 등장하는 개념입니다. 컴퓨터는 두 가지의 디지털 값(0과 1)을 입력해 하나의 값을 출력하는 회로가 모여 만들어지는데, 이 회로를 GATE(게이트)라고 합니다. 그리고 XOR를 표로 나타낸 것을 진리표라고 합니다.
1. AND GATE

# 위 예시를 python으로 제작을 해보겠습니다.
# w1, w2는 가중치(weight)를 의미하는 변수입니다.
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1*w1 + x2*w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1AND(0, 0) = 0
AND(1, 0) = 0
AND(0, 1) = 0
AND(1, 1) = 1
2. NAND GATE

def NAND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1*w1 + x2*w2
if tmp <= theta:
return 1 ## only change here
elif tmp > theta:
return 0 ## only change hereAND(0, 0) = 1
AND(1, 0) = 1
AND(0, 1) = 1
AND(1, 1) = 0
3. OR GATE

def OR(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.3 ## only change here
tmp = x1*w1 + x2*w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1 AND(0, 0) = 0
AND(1, 0) = 1
AND(0, 1) = 1
AND(1, 1) = 1
4. XOR GATE
- XOR(1, 1) = 0
- XOR(1, 0) = 1
- XOR(0, 1) = 1
- XOR(0, 0) = 0
그럼 A와 B중 1개씩만 1인경우는 어떻게 할까요?
여기서 퍼셉트론의 한계가 나타납니다.
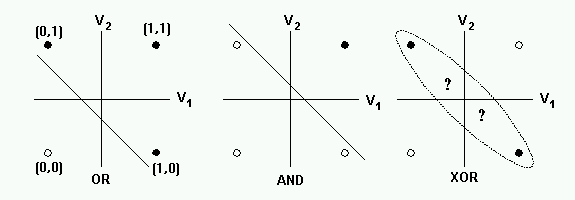
위의 진리표를 각각 그래프로 좌표 평면에 나타낸 그림 입니다. 결괏값이 0이면 흰점, 1이면 검은점입니다.
AND(반대로 NAND)과 OR 게이트는 직선을 그어 결괏값이 1인 값(검은점)을 구별할 수 있습니다.
그러나 XOR의 경우 선으로는 구분할 수 없습니다.
XOR 한계를 해결하는 방법은 바로 1차원인 좌표 평면 자체에 변화를 주는 것 입니다.
퍼셉트론의 한계가 발표된 이후 10년이 지난 후에 이 문제가 해결되는데 그 개념이 바로 다층 퍼셉트론(multilayer perceptron)입니다. 다층퍼셉트론은 여러 개의 퍼셉트론을 층 구조로 구성한 신경망 모델입니다.
XOR 문제를 해결하기 위해서는 두 개의 퍼셉트론을 한 번에 계산할 수 있어야 하는데, 이를 가능하게 하려면 숨어있는 층, 은닉층(Hidden layer)을 만들면 됩니다. 은닉층을 만들어 공간을 왜곡하면 두 영역을 가로지르는 선을 만들 수 있습니다.

'딥러닝 (Deep Learning) > 딥러닝 기초' 카테고리의 다른 글
| 딥러닝의 개념과 동작 원리 (0) | 2021.04.22 |
|---|---|
| '표현(representation)을 학습하다' 의미 (0) | 2021.04.21 |
| 활성 함수(Activation Function) 비교 (0) | 2021.04.11 |
| 신경망의 구성, 구조 with python (0) | 2021.04.11 |
| 신경망 관련 개념 정리 (0) | 2021.04.08 |